Propriétés des solutions aqueuses et pression osmotique
Table des matières
- 1. Introduction
- 2. Expression de la concentration d’une solution aqueuse
- 3. Solutions ideales et solutions non ideales : lois de Raoult
- 4. Une propriete primordiale des solutions en physiologie : la pression osmotique
- 5. Expression empirique de la pression osmotique : la loi de van ’t Hoff
- 6. Cinetique du phenomene d’osmose : cas d’une membrane hemipermeable
- 7. Cinetique du phenomene d’osmose : cas d’une membrane non parfaitement hemipermeable
I. PROPRIÉTÉS DES SOLUTIONS aqueuses Et pression osmotique
La lecture intégrale du chapitre précédent n’est pas indispensable à la compréhension de ce chapitre. Toutefois, il faut savoir ce qu’est une mole et ce que sont les états de l’eau et lire ce qui s'y rapporte dans le chapitre I.1.
Note 1 : Deux abréviations seront souvent utilisées : « DRPe », pour « Domaine des relations plantes-eau » et « CSPA » pour : Continuum Sol-Plante-Atmosphère.
Note 2 : Les termes nouveaux sont indiqués en italique, de couleur bleue
Retour aux contenus
I.1 Expression de la concentration d’une solution aqueuse
Une solution aqueuse est un mélange homogène liquide de deux ou plusieurs espèces chimiques. Elle est dite aqueuse si le solvant est l’eau. Le solvant est le composé le plus abondant. Les solutés sont les substances dissoutes.
- On parle de solution dans le cas d’une phase liquide contenant plusieurs substances dont l’une, le solvant, est traitée différemment des autres, appelées solutés, lesquels sont généralement, hors solution, des solides.
- Dans un mélange, au contraire, tous les composants sont considérés de la même manière.
Une solution est donc un mélange pour lequel on s’intéresse surtout à l’un des constituants, le solvant. Il s’agit dans le cas du DRPe, de l’eau.
Les solutions sont principalement caractérisées par la quantité et la nature des solutés qu’elles contiennent. Il existe plusieurs façons d’exprimer la quantité de solutés présente dans une solution : concentration, fraction pondérale ou volumique, fraction molaire, molarité, molalité, etc. Les unités les plus couramment utilisées dans le DRPe sont :
§ La molarité ou concentration molaire (fig. 1)
C’est la quantité de soluté (exprimée en moles) par unité de volume de la solution (et non du solvant seul). Elle s’exprime le plus souvent en moles par litre (mol l-1). Ainsi, une concentration 0,6 molaire contient 0,6 mole de soluté par litre de solution. Une solution contenant 1mole de soluté par litre est appelée solution normale. On obtient des solutions de même concentration (mol l-1) en dissolvant 1 mole (40g) de soude (NaOH) dans 0,5 litre d’eau, ou 3 moles (120 g) dans 1,5 litre. Dans les deux cas la molarité est de 2 mol l-1.
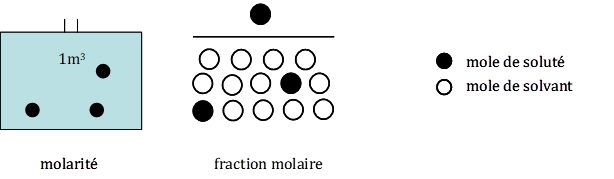
Figure 1. Deux expressions habituelles de la concentration d’une solution : la molarité et la fraction molaire. La molarité s’exprime le plus souvent en moles par litre. La fraction molaire est le rapport du nombre de moles de soluté sur le nombre total de moles de la solution. C’est donc un rapport sans dimension. Plus la solution est diluée plus la fraction molaire se rapproche du rapport du nombre de moles de soluté sur le nombre de moles de solvant.
§ La fraction molaire (fig. 1)
La fraction molaire, Ni, du composant i, est égale au rapport du nombre de moles ni de ce composant au nombre total (n1 + n2 +…nn ) de moles des n composants de la solution, soit :
Ni = ni / (n1 + n2 +….nn) = ni /Sn équat. 1
La fraction molaire est un nombre sans dimension ; elle ne peut être qu’inférieure ou égale à 1. Une fraction molaire de 1 signifie que l’on a, soit de l’eau pure, soit du soluté pur. Quand on parle de fraction molaire, c’est la plupart du temps pour définir la concentration d’une solution en ne prenant en compte qu’un seul soluté. Dans ces conditions, une molarité de 1 mole L-1 correspond à une fraction molaire de : (1/(1+nombre de moles d’eau par litres).
La mole d’heau pesant 18 g, le nombre de moles d'eau par litre est égal à 1000/18 = 55,5. La fraction molaire est donc dans ce cas égale à 1/56,5= 0,01768
Le « pourcentage molaire » est égal à 100 Ni.
Application 1. Une solution « 2molaires », jugée en général assez concentrée chez les végétaux, ne correspond en réalité qu’à une faible fraction molaire de soluté : 2/57,55 soit 0,035. La fraction molaire de l’eau est le complément, soit 0,965.
Application 2. Expression des grandeurs ci-dessus pour une solution sucrée contenant 40 g de saccharose dans 1 litre (~ 1000g) de solution :
- fraction molaire de ce mélange : le poids d’une mole de saccharose étant de 342 g, 40 g représentent 40/342 = 0,117 mole ; de même, 1000 g d’eau représentent 55,555 moles d’eau. La fraction molaire du saccharose dans cette solution est donc de 0,117/ (55,555 + 0,117) = 0,0021 ; pour l’eau cette fraction molaire est le complément à 1 soit : 55,555/ (55,555 + 0,117) = 0,998.
- molarité : 0,117/1 = 0,117 mole.l-1
§ La molalité
La notion de « molalité » est voisine de celle de « molarité »: c’est la concentration exprimée par le nombre de moles de soluté dans 1000 g de solvant et non de solution. Elle s’exprime en mol kg-1. La molalité intervient dans les constantes ébulliométrique et cryoscopique des lois de Raoult (voir ci-après). Molalité et molarité s’expriment par des nombres d’autant plus voisins que la densité du liquide est proche de 1 d’une part (cas de l’eau), et que d’autre part les solutions sont peu concentrées. Les poids étant plus faciles à mesurer que les volumes, la molalité est plus facile à obtenir que la molarité et, contrairement à la molarité, elle est indépendante de la température.
À la température ordinaire, les solutés sont bien souvent des solides : c’est le cas par exemple du sucre ou du sel de cuisine (chlorure de sodium) par exemple. Ce dernier est formé d’ions de signes contraires (anion : Cl- ; cation : Na+) qui, dans un cristal, sont très fortement liés, comme en témoigne la température élevée de fusion du sel, 800°C). Or il suffit de le mettre dans l’eau à la température ordinaire pour qu’il s’effondre ! C’est dire l’importance des forces qui peuvent être mises en jeu dans la dissolution.
La quantité maximale de substances que l’on peut dissoudre dans un solvant donné est caractéristique de chaque soluté, pour une température et une pression données. Ainsi par exemple dans un litre d’eau à 0°C on ne peut dissoudre que 365 g de chlorure de sodium, alors que l’on peut dissoudre 1790 g de saccharose. Si l’on dépasse la limite correspondant à chaque corps, le soluté ne se dissout plus : la solution est alors dite saturée.
Retour aux contenus
I.2 Solutions idéales et solutions non idéales : lois de Raoult
Nous avons vu au chapitre I.1 qu’un gaz parfait, par définition, suit la loi de Boyle-Mariotte. On a utilisé la même démarche pour comprendre les propriétés des solutions liquides en définissant un modèle de « solution idéale », dans lequel les molécules de soluté se comportent comme les molécules de gaz dans les gaz parfaits, c’est à dire qu’elles n’ont pas d’interaction entre elles. Ce modèle, décrit par les lois de Raoult (explicitées ci-dessous), prévoit un comportement spécifique de la solution idéale. Dans la réalité, les solutions qui s’en rapprochent le plus sont celles pour lesquelles les interactions de molécules de solutés, entre elles ou avec celles du solvant, sont négligeables. On estime que, statistiquement, il y a dans une telle solution environ 10 molécules d’eau entre deux molécules de soluté (Atkins, 2000).
Le comportement des solutions dépend de la nature et de la concentration de leurs constituants, solvant et solutés. Les solutés peuvent être ou non volatils. Les solutés non volatils ne sont pas présents dans la phase gazeuse en équilibre avec la solution, contrairement aux solutés volatils (ex : l’alcool) qui présentent une pression de vapeur. Dans le DRPe nous n’aurons affaire qu’au solvant « eau » et nous nous limiterons au cas le plus simple et le plus fréquent où les solutés sont en concentration relativement faible.
La présence de solutés dans l’eau modifie des propriétés physiques comme la température de congélation (ou de fusion de la glace) ou la pression de vapeur en équilibre. Examinons ce qu’il se passe lorsqu’on place de l’eau pure dans une enceinte fermée isotherme à la température T constante (Fig. 2). L’eau s’évapore jusqu’à ce que la pression de vapeur dans la phase gazeuse atteigne une valeur maximale dite pression de vapeur saturante ![]() pour la température correspondante. La même expérience faite avec une solution, sucrée ou salée par exemple, conduira, à l’équilibre, à une pression de vapeur p’eau inférieure. Cette baisse de pression de vapeur est d’autant plus forte que la concentration du soluté est grande. Dans ce qui suit nous nous limiterons au cas simple d’une solution « idéale » à deux constituants (un solvant volatil, l’eau, et un soluté non volatil).
pour la température correspondante. La même expérience faite avec une solution, sucrée ou salée par exemple, conduira, à l’équilibre, à une pression de vapeur p’eau inférieure. Cette baisse de pression de vapeur est d’autant plus forte que la concentration du soluté est grande. Dans ce qui suit nous nous limiterons au cas simple d’une solution « idéale » à deux constituants (un solvant volatil, l’eau, et un soluté non volatil).

Figure 2. Equilibre de la vapeur d’eau avec de l’eau pure ou une solution aqueuse. Si on place de l’eau pure dans une enceinte fermée à température constante T, l’eau s’évapore jusqu’à ce que la pression de vapeur dans la phase gazeuse atteigne une valeur maximale dite « pression de vapeur saturante » ![]() pour la température correspondante. Avec une solution, sucrée ou salée par exemple, l’équilibre est atteint pour une pression de vapeur p’eau inférieure. Les mêmes phénomènes s’observent avec tous les solvants.
pour la température correspondante. Avec une solution, sucrée ou salée par exemple, l’équilibre est atteint pour une pression de vapeur p’eau inférieure. Les mêmes phénomènes s’observent avec tous les solvants.
· Loi de Raoult sur la pression de vapeur du solvant (eau)
Dans une solution idéale, la pression de vapeur du solvant en équilibre avec la solution p’solvant est proportionnelle à la fraction molaire Nsolvant du solvant dans la solution :
![]()
Cette loi simple, dite loi de Raoult permet de définir la notion de solution idéale. Pour l’eau elle devient :
![]() équat. 2
équat. 2
p’eau = pression de vapeur d’eau en équilibre avec la solution (Pa ou MPa)
![]() = pression de vapeur saturante de l’eau (Pa ou MPa)
= pression de vapeur saturante de l’eau (Pa ou MPa)
Neau = fraction molaire de l’eau dans la solution (nombre sans dimensions, inférieur ou égal à 1)
· Abaissement de la pression de vapeur en fonction de la concentration du soluté.
Dans un mélange à deux constituants, Neau + Nsoluté = 1 , la loi précédente s’écrit donc aussi :
![]() équat. 3
équat. 3
ou bien : ![]()
d’où encore :
![]() équat. 4
équat. 4
L’abaissement de la pression de vapeur, Dp, est donc proportionnel à la fraction molaire du soluté Nsoluté (Fig. 3).
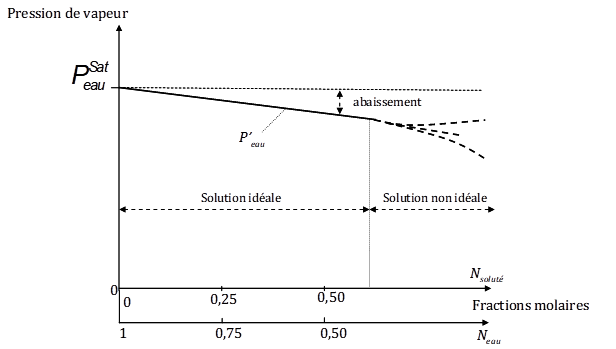
Figure 3. Variation de la pression de vapeur d’eau p’eau , en équilibre avec une solution aqueuse en fonction de la fraction molaire du soluté Nsoluté. La figure montre que l’on peut distinguer deux domaines : a) solution idéale (diluée) : p’eau varie linéairement avec Nsoluté ; b) solution non idéale : au delà d’une certaine fraction molaire la relation cesse d’être linéaire.
Application : quelle est à 25°C, la pression de vapeur de l’eau en équilibre avec une solution aqueuse de sucre (saccharose) dont la molarité est égale à 2 moles par litre de solution, sachant que la pression de vapeur saturante de l’eau à 25°C est de 2,339 kPa ?
Pour appliquer la formule 2 ci-dessus, il faut calculer la fraction molaire de l’eau, Neau. Celle-ci vaut : 55,555/(2,000 + 55,555) = 0,965. La pression de la vapeur d’eau p’eau en équilibre avec cette solution est donc de 2,339 x 0,965 = 2,257 kPa. Cet abaissement est très faible et même négligeable pour un grand nombre d’applications.
Les solutions concentrées ou qui contiennent des électrolytes s’écartent plus ou moins des solutions idéales.
Les solutions idéales ont d’autres propriétés générales dites aussi colligatives c’est-à-dire fonction uniquement du nombre de particules de soluté(s) et non de leur nature chimique. Ces propriétés découlant directement de la loi de Raoult ci-dessus, on les désigne souvent sous l’appellation de lois de Raoult, au pluriel. Deux autres lois existent en effet, outre celle qu’on vient de voir sur l’abaissement de la pression de vapeur du solvant (équat. 4). L’une concerne l’élévation de la température d’ébullition et l’autre l’abaissement du point de congélation (ou abaissement cryoscopique) qui seul nous intéresse ici (Fig. 4).
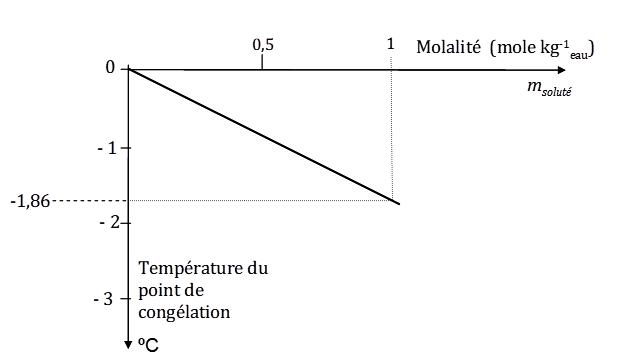
Figure 4. Abaissement du point de congélation d’une solution suivant la loi de Raoult : une solution molaire gèle à -1,86 °C. Nota : pour le sel, NaCl, cela correspond à 58,44g par kg d’eau.
L’abaissement de la température de congélation lié à la présence d’un soluté est donné par la formule ci-dessous :
![]() équat. 5
équat. 5
avec :
DTcongélation : abaissement du point de congélation (°C)
kc : constante cryoscopique du solvant (°C mol-1(soluté) kg (solvant))
msoluté : molalité du soluté (mol de soluté par kg de solvant)
i : coefficient de dissociation du soluté ou coefficient de van ’t Hoff (sans dimension).
Ce coefficient vaut par exemple 2 pour du chlorure de sodium NaCl qui est complètement dissocié en solution aqueuse et serait voisin de 3 pour le chlorure de magnésium, MgCl2 qui se dissocie de façon incomplète en ions Mg++ et Cl-.
La constante cryoscopique (1,86 °C mol-1 kg pour l’eau) est une caractéristique du solvant : elle ne dépend pas de la nature du soluté. On voit que pour une solution aqueuse de molalité égale à 1 mole kg-1 (molarité ![]() 1) l’abaissement du point de congélation est de 1,86 °C. Une telle solution ne gèlera donc pas au dessus de – 1, 86°C.
1) l’abaissement du point de congélation est de 1,86 °C. Une telle solution ne gèlera donc pas au dessus de – 1, 86°C.
Remarque 1. Les solutions dont il est question dans le DRPe, comme la solution du sol, les sèves (xylémienne, phloémienne), etc., peuvent contenir un grand nombre de solutés différents. On constate cependant que tant que la concentration globale de ces solutés reste faible - ce qui est le cas de loin le plus fréquent, leur comportement reste très proche de celui des solutions idéales auxquelles on peut donc les assimiler.
Remarque 2. Lorsque plusieurs solutés sont en mélange il convient de prendre en compte la fraction molaire cumulée de l’ensemble des solutés en tenant compte du taux de dissociation de chacun.
Remarque 3. Le salage des routes enneigées en hiver donne un exemple de ce qui peut se passer pour de grandes concentrations de soluté. En application de la loi ci-dessus, le fait d’apporter du sel sur la neige entraîne la fonte de celle-ci, le mélange ainsi constitué possédant un point de congélation inférieur à zéro. La température de congélation sera d’autant plus basse que la concentration en sel sera grande. Une mole de sel (NaCl) correspond à 58,44 g. Si l’on considère la neige salée comme une solution, elle se sature avec 357 g de sel par litre soit une molalité d’environ 6,1 mol kg-1; en appliquant la loi ci-dessus avec un coefficient de dissociation de 2, on trouve que la neige reste liquide jusqu’à environ -20,2°C.
Sur un autre plan, il faut souligner que le salage amène à déverser d’importantes quantités de sel, ce qui est très dommageable aux racines des arbres.
§ Diagramme de phase d’une solution idéale
Le diagramme de phases de l’eau est un graphique qui exprime son état (solide, liquide ou vapeur) en fonction de sa température et de sa pression. Un tel diagramme existe pour toute solution aqueuse : il est simplement décalé par rapport à celui de l’eau pure (fig. 5). On y retrouve bien les propriétés ci-dessus : pour une pression donnée, le point d’ébullition est plus élevé et le point de fusion est abaissé. Ces modifications sont proportionnelles à la concentration de la solution.
Remarque. Les changements de propriétés d’une solution par rapport au solvant pur s’expliquent au niveau moléculaire, notamment dans les interactions entre solvant et soluté, non abordées ici.
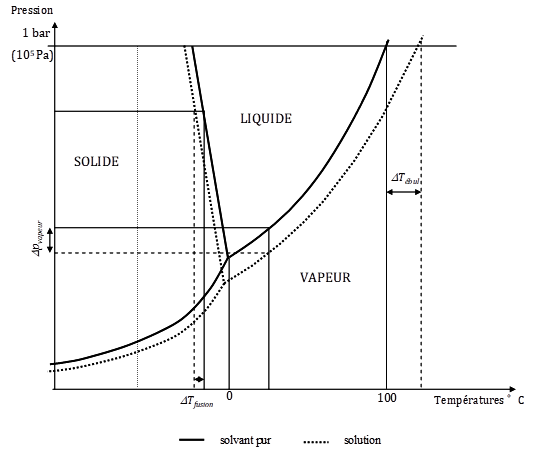
Figure 5. Diagramme de phases d’un solvant pur (eau, trait plein) et d’une solution aqueuse (traits pointillés). On retrouve les trois lois de Raoult : l’abaissement de la pression de vapeur en équilibre pour une température donnée (Dpvap), l’abaissement du point de congélation (DTfusion) et l’augmentation de la température d’ébullition (DTébul). Le diagramme de phases de l’eau pure a été présenté au chapitre I.1.
Retour aux contenus
I.3 Une propriété primordiale des solutions en physiologie : la pression osmotique P
Comme les molécules d’un gaz, les molécules de soluté ont tendance à se disperser dans tout le volume de la solution. Ce processus, directement lié à l’agitation thermique est appelé diffusion. Il conduit à homogénéiser la répartition des molécules dans la solution. Que se passe-t-il si l’on sépare cette solution en deux compartiments A et B (Fig. 6), en installant une membrane semi-perméable M c’est à dire étanche au soluté mais que le solvant peut franchir ? Ce dispositif appelé osmomètre, déclenche le phénomène d’osmose. L’osmose est le passage spontané d’un solvant pur, depuis le compartiment dilué vers le compartiment concentré, lorsque ces deux compartiments sont séparés par une membrane hémiperméable (ou semi-perméable), c’est-à-dire perméable au solvant seul. Dans le DRPe, le solvant est l’eau.
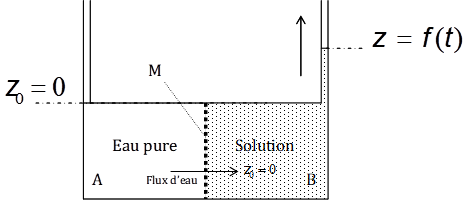
Figure 6. Principe du phénomène d’osmose. Les deux compartiments A et B sont séparés par une membrane semi-perméable. L’eau du compartiment A traverse la membrane jusqu’à obtention d’un équilibre dans lequel la pression hydrostatique en B équilibre l’effet de la pression osmotique.
|
Figure 7. Dispositif utilisé par Dutrochet pour l’étude de l’osmose. Cet osmomètre, très imparfait, utilisait une membrane animale (vessie de porc). |
· L’expérience de base et son interprétation
Considérons l’osmomètre dans une version moderne (fig. 8). Dans un large récipient A rempli d’eau, on plonge un tube de petite section, dont l’extrémité inférieure B, élargie, est fermée par une membrane M, rigide et hémiperméable. Le tube et sa base élargie sont remplis d’une solution dont le soluté (par exemple du glucose) ne peut traverser la membrane. Les conditions de départ sont les suivantes : la température est uniforme et constante, la concentration initiale Co est connue, le niveau z de la solution dans le tube est le même que celui de l’eau dans le récipient A. Au niveau de la membrane, la pression hydrostatique est donc la même, à l’extérieur comme à l’intérieur de la partie évasée. Voyons maintenant le déroulement de l’expérience et ce que l’on peut en déduire.
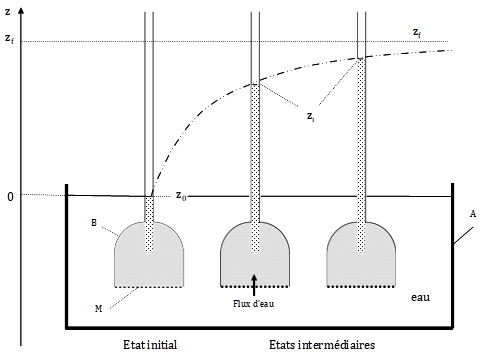
Figure 8. Cinétique de l’osmose. Un récipient A contient de l’eau. On y plonge un tube dont la base élargie, B, contient une solution dont le soluté ne peut pas passer à travers la membrane semi-perméable M. Etat initial : les niveaux de l’eau dans A et dans B sont les mêmes. Etat intermédiaire, le niveau est monté à zi. Etat final, le niveau atteint une valeur maximale, zf. Ce niveau donne la valeur de la pression hydrostatique équivalente à la pression osmotique p de la solution dans B.
a. Une fois le dispositif mis en place, on observe que le niveau monte dans le tube : il y a entrée d’eau de A vers B.
b. Après un certain temps, le niveau se trouve à une hauteur zi. L’eau continue à pénétrer dans le tube B contre une différence de pression hydrostatique P (celle exercée par la colonne de solution du tube) égale à :
![]() équat. 6
équat. 6
Dp = différence de pression (Pa)
ρsolution = masse volumique de la solution (kg m-3)
g = accélération de la pesanteur (9,81 m s-2)
zi = hauteur intermédiaire de la solution dans le tube (m)
z= hauteur initiale de la solution (m)
c. Avec le temps le niveau monte de moins en moins vite. La hauteur de la solution finit par se stabiliser à une certaine hauteur maximale zf. La différence de pression hydrostatique de part et d’autre de la membrane est alors de :
![]() équat. 6’
équat. 6’
Remarque. Dans la réalité, le déroulement de cette expérience peut se trouver perturbé par divers phénomènes non pris en compte dans cette présentation : dilution de la solution dans le tube B au fur et à mesure que l’eau y pénètre donc diminution de la pression osmotique en B, ou membrane non parfaitement hémiperméable par exemple.
Que peut-on conclure de cette expérience ?
i) L’entrée d’eau dans le tube B s’effectue à tout moment dans le sens inverse de celui attendu. En effet, en raison de la différence de pression hydrostatique due à l’eau dans le tube, on s’attendrait à ce que l’eau aille du tube vers le récipient !! du fait de la différence de pression hydrostatique Dp, d’ailleurs nulle au départ. Si l’on augmente la concentration initiale de la solution dans B et qu’on répète l’expérience, le niveau final atteint est plus élevé. On peut donc dire que l’origine du mouvement d’eau comme le niveau final de la solution dépendent de l’écart de concentration entre les deux compartiments A et B, de part et d’autre de la membrane.
ii) Tout se passe comme si la solution en B exerçait une « succion » (pression négative) sur l’eau pure, succion qui ne s’annule que lorsqu’elle est équilibrée par l’augmentation de pression hydrostatique dans le tube.
iii) Un équilibre est atteint lorsque l’entrée d’eau s’arrête au niveau zf. La différence de pression hydrostatique est alors égale à DPfinale (équat. 6’). On appelle pression osmotique de la solution, notée p , cette pression hydrostatique finale qui équilibre la succion de la solution.
p = DPfinale = r g zf équat. 7
Conventionnellement, elle est comptée positivement et s’exprime en pascals (Pa) ou MPa. La pression osmotique ne se manifeste qu’en présence d’une membrane hémiperméable. L’eau pure a une pression osmotique nulle par définition.
Retour aux contenus
I.4. Expression empirique de la pression osmotique : la loi de van ’t Hoff
C’est en se basant sur les résultats de Pfeffer que van ’t Hoff émit en 1887 l’hypothèse (géniale !) que la pression osmotique d’une solution est analogue à la pression d’un gaz parfait et obéit à la même loi (PV = nRT, cf. chapitre I.1), les molécules de soluté remplaçant les molécules de gaz. Dans les deux cas la pression est proportionnelle à la concentration des particules (molécules de gaz ou de soluté) et à la température absolue. En réalité, cette affirmation n’est vérifiée en général, que pour des concentrations faibles. La pression osmotique d’une solution peut donc s’écrire, de façon simplifiée :
p = nRT / V = c RT équat. 8
p = pression osmotique de la solution (Pa)
n = nombre de moles du soluté (sans dimension)
R = constante des gaz parfaits (8,314 J mol-1 K-1)
T = température absolue (K)
V = volume de la solution (m3)
c = n/V = concentration molaire totale (mol m-3)
La loi de van ’t Hoff, indique que la pression osmotique d’une solution est proportionnelle à sa concentration. Elle montre aussi qu’à une température donnée, toutes les solutions idéales de même concentration molaire ont la même pression osmotique : p est indépendante de la nature du solvant et du soluté, tout comme la pression est indépendante de la nature des gaz dans la loi de Boyle-Mariotte. Seules les concentrations interviennent.
Certaines solutions (électrolytes) conduisent le courant électrique par suite d’une dissociation plus ou moins complète des molécules en ions positifs et négatifs, de sorte que le nombre de particules présentes dans la solution est supérieur au nombre de moles. La dissolution d’une mole de NaCl dans l’eau par exemple, entraine la dissociation complète en ions Na+ et Cl-, d’où un nombre de particules double. Dans ce cas la loi de van’t Hoff s’applique à condition de tenir compte de leur degré de dissociation. On écrit :
p = niRT / V = ciRT
où i est un facteur de dissociation, compris entre 1 (absence de dissociation) et 2 (molécules pleinement dissociées). L’exercice d’application 3 ci-dessous illustrera ce principe.
Remarque. Nous allons tenter de donner une vision simplifiée du phénomène d’osmose et de la notion de pression osmotique en explicitant l’analogie entre le comportement des molécules d’un gaz et celui des molécules d’un soluté au sein d’un solvant qui est à la base du raisonnement de van ‘t Hoff. Nous utiliserons pour ce faire la notion aujourd’hui abandonnée de « pression de diffusion », notion insuffisamment rigoureuse sans doute, mais qui a le mérite à notre sens de bien faire comprendre le phénomène.
La théorie cinétique des gaz postule que les molécules d’un fluide sont soumises à une agitation thermique et que la pression hydrostatique est la résultante des chocs des molécules entre elles. Reprenons nos deux compartiments A et B (figure 6 et 8) séparés par une membrane hémiperméable ; A contient de l’eau pure et B une solution de glucose par exemple. En début d’expérience la pression hydrostatique totale est identique en A et en B et égale à la pression atmosphérique Patm. Supposons la concentration de sucre suffisamment faible pour que les chocs des molécules de glucose entre elles soient relativement peu fréquents, comme c’est le cas pour les molécules d’un gaz. Les molécules de glucose ne traversent pas la membrane mais elles contribuent pour leur part à la pression totale exercée sur cette membrane côté B ; cette part est grosso modo égale à la fraction molaire du soluté. Appelons « pression de diffusion » cette pression des molécules de glucose que nous noterons p. Il s’agit d’une notion analogue à la pression partielle d’un gaz dans un mélange gazeux. Nous dirons que la pression des molécules d’eau en B est égale à Patm - ǀpǀ alors qu’en A où elles sont seules, leur pression de diffusion est égale à la pression totale Patm. C’est cette différence de pression de diffusion des molécules d’eau de part et d’autre de la membrane qui explique le mouvement global d’eau de A vers B. L’équilibre est atteint et le mouvement d’eau s’arrête lorsque la pression de diffusion des molécules d’eau devient égale dans les deux compartiments ce qui suppose que la pression hydrostatique totale soit plus grande côté B, d’où l’élévation du niveau d’eau. La formule de van ‘t Hoff exprime en outre que, comme pour les gaz parfaits, la « pression de diffusion » des molécules de soluté est proportionnelle à leur concentration n/V (tout au moins pour les faibles concentrations) et à l’agitation thermique (facteur T). Une approche plus moderne et rigoureuse mais plus abstraite du phénomène devrait faire appel à la notion de potentiel chimique de l’eau.
Application 1. Calculer la pression osmotique d’une solution de saccharose de concentration 0,6 mole par litre, à la température de 20°C.
On a c = 0,6 mol l-1 ; T = 293,15 K et R = 0,08314 bar mol-1l K-1. La pression osmotique est donc égale à : p = 0,6 x 0,0831 x 293,15 = 0,6 x 24,37 = 14.6 bars
Application 2. Calculer la variation relative de la pression osmotique d’une solution entre 0°C (soit 273 °K) et 25 °C (soit 298 °K). De la relation 8 on tire :
![]()
L’augmentation de pression due à la différence de température est donc d’environ 10 % pour un écart de température de 25°C.
Application 3. Calculer la pression osmotique de l’eau de mer en supposant qu’elle contient 35 grammes de chlorure de sodium, NaCl, par litre. Ce cas illustre un fait important : on doit tenir compte du degré de dissociation en ions pour calculer la pression osmotique d’une solution ionisée. Dans une solution de glucose il n’y a pas d’ions, il n’y a que des molécules de glucose. Par contre dans l’eau de mer, les molécules de chlorure de sodium n’existent pas : seuls existent des ions Na+ et Cl- . On parle d'osmole pour désigner une concentration en particules osmotiquement actives dans une solution. Ici, du point de vue osmotique une concentration molaire de NaCl correspond donc à une concentration de 2 moles de soluté par litre (2 osmoles).
La masse d’une mole de NaCl est de 58,4 g ; 35 g représentent donc 35/58,4 = 0,60 mole, soit une concentration c = 1,2 osmoles par litre. A 20°C, la pression osmotique de cette solution de NaCl vaut donc p = 1,2 x 2,437 = 2,92 MPa ou 29,2 bars.
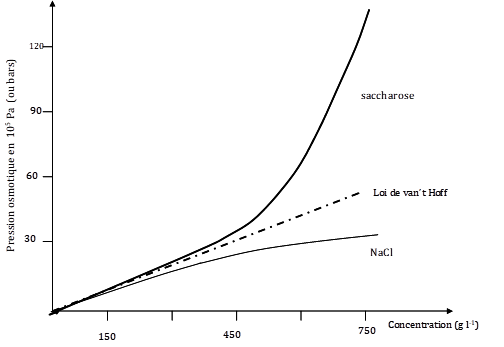 Figure 9. Pressions osmotiques calculées par la loi de van t’Hoff (en pointillé) et mesurées expérimentalement (trait plein) pour des solutions de saccharose à différentes concentrations. Pour ce soluté, la loi de van t’Hoff ne s’applique que jusqu’à des concentrations d’environ 150 gL1 soit environ 0,43 molaire (Duclaux, 1938). D’autres solutés comme le chlorure de sodium ont par contre des pressions osmotiques inférieures à celles données par la loi de van t’Hoff.
Figure 9. Pressions osmotiques calculées par la loi de van t’Hoff (en pointillé) et mesurées expérimentalement (trait plein) pour des solutions de saccharose à différentes concentrations. Pour ce soluté, la loi de van t’Hoff ne s’applique que jusqu’à des concentrations d’environ 150 gL1 soit environ 0,43 molaire (Duclaux, 1938). D’autres solutés comme le chlorure de sodium ont par contre des pressions osmotiques inférieures à celles données par la loi de van t’Hoff.
La figure 9 donne une idée du domaine de validité de la loi de van ’t Hoff pour trois composés (le saccharose, le glucose et le chlorure de sodium). On voit que pour ces 3 solutés la relation entre pression osmotique et concentration ne suit la loi de van ’t Hoff que pour des concentrations inférieures à une mole par litre environ. Pour d’autres solutés la loi peut s’appliquer jusqu’à des concentrations plus grandes. Pour certains solutés des changements importants de propriétés se manifestent aux fortes concentrations. Ainsi par exemple les solutions de polyéthylène glycol (PEG), souvent utilisées en physiologie pour provoquer un choc osmotique, ne suivent la loi de van ‘t Hoff que pour des concentrations très faibles. Pour connaître la pression osmotique de ces solutions, il faut avoir recours soit à des lois complexes, soit à l’expérimentation (fig.9).
Dans le DRPe, les solutions auxquelles on a affaire couvrent une large gamme, depuis des solutions diluées (ex : la solution du sol, hormis pour les sols salés, et la sève xylémienne, au moins pendant une partie de l’année) jusqu’à des solutions concentrées pouvant atteindre parfois 2 molaires (Tyree and Richter 1981). Exemples : suc vacuolaire de plantes adaptées à la sécheresse ou au froid, sève phloémienne, sève xylémienne hivernale chez certaines espèces (par exemple chez l’érable à sucre).
Les solutés sont, la plupart du temps sous forme d’ions. C’est le cas des sucs vacuolaire, cytoplasmique et pariétaux (voir chap. II.1), qui contiennent de nombreux ions minéraux et de nombreuses molécules organiques ionisées plus ou moins grosses porteuses de sites chargés (acides organiques, pectiques, acides nucléiques, nombreuses protéines,..). On appelle ces corps chargés électriquement des polyélectrolytes. Ces molécules ne peuvent pas sortir de la cellule mais elles perturbent la distribution des ions entre l’extérieur et l’intérieur et jouent donc un rôle dans la pression osmotique cellulaire. Elles sont à l’origine des processus de Donnan (voir complément C2 en fin de chapitre).
Retour aux contenus
I.5. Cinétique du phénomène d’osmose : cas d’une membrane hémiperméable
Attention : ce paragraphe, qu’on a cru bon de placer ici car il traduit directement l’un des aspects essentiels de l’osmose, utilise néanmoins des notions (équation 9) qui n’ont pas été explicitées jusqu’ici et qui ne le seront que plus loin.
Quels sont les facteurs qui déterminent la vitesse du processus osmotique ? Par exemple, combien de temps faut-il pour atteindre l’équilibre (arrêt du flux d’eau) ? Dans l’exemple simple qui suit, nous considérons le cas d’une membrane parfaitement hémiperméable (seules les molécules de solvant peuvent traverser la membrane). On négligera aussi l’effet de la dilution de la solution initiale, au fur et à mesure que l’eau rentre dans l’osmomètre.
On va montrer que la cinétique de remplissage du tube B, z = f(t) est une fonction exponentielle du temps à exposant négatif (fig. 10). Les lois de la diffusion permettent d’écrire l’expression du flux d’eau Jv entrant dans B :
![]() équat.9
équat.9
Avec :
Jv = flux d’eau (m3 m-2 s-1 ou encore m s-1) compté positivement quand l’eau entre dans le tube B
S = surface de la membrane (m2)
Lp = perméabilité hydraulique de la membrane (m3 s-1 MPa-1)
DP = PB – PA= ![]() la différence de pression hydrostatique entre B et A (MPa)
la différence de pression hydrostatique entre B et A (MPa)
p = pression osmotique dans B (MPa) comptée positivement
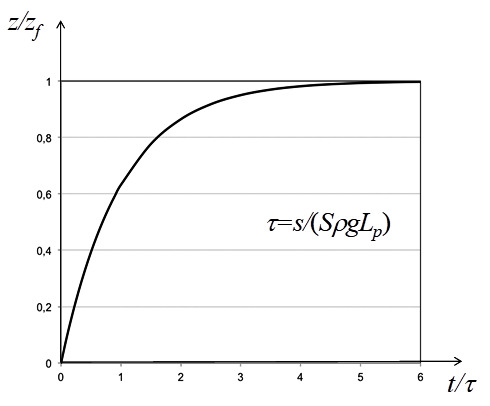
Figure 10. Forme générale d’une cinétique osmotique avec une membrane hémiperméable parfaite. On a utilisé une représentation en variables réduites soit z/zfen fonction de t/t de sorte que toutes les situations sont représentées par cette unique courbe.
L’équation 9 correspond à la définition de la notion de perméabilité Lp. Elle indique que le flux d’eau qui rentre dans le tube est proportionnel à chaque instant, à la surface de passage de l’eau (S), à la perméabilité hydraulique de la membrane à l’eau (Lp), et à la différence de pression (p - DP) qui est la force motrice qui provoque l’entrée d’eau. On suppose p constant au cours de la cinétique c’est à dire qu’on néglige l‘effet de dilution dû à l’entrée d’eau.
Pour établir la loi z(t), on va exprimer la vitesse de variation instantanée de z à partir de l’équation précédente. Soit s la section du tube B au niveau où l’on mesure les hauteurs z au dessus de l'entrée du tuvbe. Le flux Jv d’eau qui entre dans le tube pendant un court intervalle de temps dt, (c’est donc une équation différentielle) provoque une variation du niveau dz telle que :
![]()
Remplaçons Jv par son expression dans l’équation 11, on obtient l’équation différentielle suivante :
![]() équat. 10
équat. 10
Sachant que la hauteur finale zf est telle que p=rgzf (cf. équation 7), et appellons « 1/tau » l’ensemble SρgLp/s, l’équation 10 devient alors :
![]()
d’où encore :
![]()
Cette dernière équation s’intègre sous la forme
![]()
où A est une constante d’intégration dont la valeur est déterminée par la condition initiale z = 0 pour t = 0. On trouve ainsi A = -zf d’où l’expression finale de la solution :
![]() équat. 11
équat. 11
Le niveau z dans le tube s’élève donc en suivant cette loi exponentielle à exposant négatif en fonction du temps. Il tend asymptotiquement vers la hauteur finale zf, directement fonction de la pression osmotique initiale. La figure 10 montre une représentation adimensionnelle de cette fonction, c’est à dire qu’elle représente la variation de z/zf en fonction de t/t . On voit que lorsque t/t= (soit t=t), le niveau z vaut environ 0,63 zf et que z vaut plus de 0,99 zf lorsque t=5t; autrement dit, on est pratiquement à l’équilibre.
La cinétique du phénomène est déterminée par la constante de temps t qui ne dépend pas de p mais du rapport des surfaces s/S et de la perméabilité hydraulique Lp de la membrane. Plus s/S est petit ou plus Lp est grand, plus t est petit, et plus la hauteur finale est donc atteinte rapidement.
Application. Soit, par exemple, une solution de glucose à 20°C et ayant une concentration de 5.10-3 moles par litre. La pression osmotique vaut p = cRT = 5.10-3 x 2,437 l MPa mol-1 = 0,0122 MPa, soit une hauteur finale d’eau, zf = p/rg d’environ 0,0122 x 102 m = 1,24 m en prenant ρs=1000 kg m‑3 et g=9,81ms‑2 . Considérons par ailleurs les caractéristiques suivantes de la membrane : S = 10 cm2, et Lp=3,5 10‑11m s‑1Pa‑1. Soit enfin s = 0.01 cm2 la section du tube manométrique. La constante de temps t vaut 582 secondes et l’équation 11 devient alors : ![]() en mètres. La courbe correspondante est représentée sur la figure 11, parmi d’autres exemples pour trois autres valeurs de la constante de temps.
en mètres. La courbe correspondante est représentée sur la figure 11, parmi d’autres exemples pour trois autres valeurs de la constante de temps.
Les membranes hémiperméables parfaites n’existent pas dans la réalité. Certaines produites par l’industrie ont un comportement approchant. Les membranes biologiques pour lesquelles la perméabilité vis à vis de telle molécule ou tel ion est le fruit d’un contrôle physiologique se comportent comme des membranes semi-perméables.
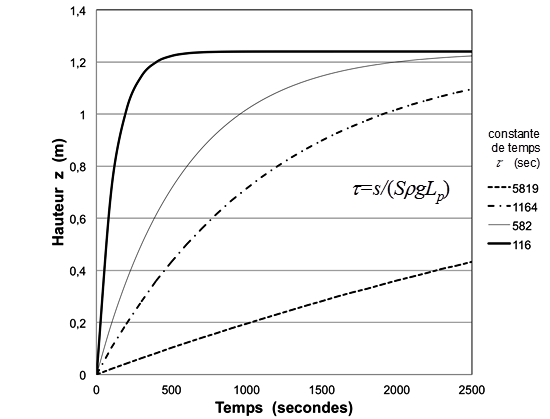
Figure 11. Quatre exemples de cinétique osmotique montrant l’influence de la constante de temps t (voir texte).
Retour aux contenus
I.6. Cinétique du phénomène d’osmose : cas d’une membrane non parfaitement hémiperméable
C’est le cas des membranes biologiques. Revenons au schéma de l’osmomètre : la membrane n’est pas parfaitement étanche au soluté qui passe donc plus ou moins facilement du tube B vers le réservoir d’eau A (fig.12) de sorte que la différence de concentration de part et d’autre de la membrane diminue au cours du temps. La concentration initialement nulle dans A va donc croître régulièrement. A l’équilibre, les concentrations de glucose seront les mêmes dans les deux compartiments et le niveau final dans le tube sera égal au niveau de départ zf = zo.
On peut, comme précédemment, établir la cinétique du phénomène à condition de prendre en compte la perméabilité de la membrane aux molécules de soluté et le volume respectif du récipient A et de l’osmomètre B. La figure 13 illustre qualitativement la différence de cinétique du phénomène d’osmose dans le cas d’une membrane hémiperméable et dans celui d’une membrane non hémiperméable. Les deux membranes sont supposées avoir une perméabilité identique pour l’eau. Trois différences principales apparaissent entre ces deux cas :
- le flux initial est plus lent dans le cas de la membrane non hémiperméable,
- la hauteur d’eau maximale atteinte est inférieure au cas précédent et elle ne correspond plus à une situation d’équilibre.
- à l’état final, la hauteur zf est nulle, ce qui exprime que la différence de concentration de part et d’autre, entre l’intérieur (le tube B) et l’extérieur, est nulle.
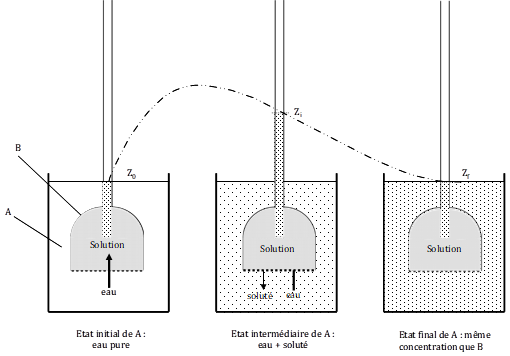
Figure 12. Cinétique d’entrée de l’eau dans le cas d’un osmomètre dont la membrane n’est pas hémiperméable : le soluté de B diffuse dans le récipient A en même temps que l’eau de A pénètre dans B. La hauteur maximale atteinte est inférieure à la hauteur zf précédente. Cette hauteur n’est pas un point d’équilibre mais simplement un état transitoire. Avec le temps, le niveau dans le tube redescend pour revenir à la hauteur de départ. A ce moment, la concentration du liquide dans A est la même que dans B.
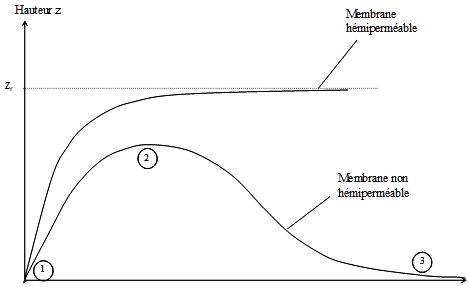
Figure 13. Comparaison des cinétiques d’entrée d’eau dans l’osmomètre pour une membrane hémiperméable parfaite et une membrane non hémiperméable. Les deux membranes sont supposées avoir la même perméabilité à l’eau Lp. Le fait que la membrane n’est pas hémiperméable (elle laisse passer le soluté) entraine 1) une entrée d’eau au départ plus lente ; 2) une hauteur maximale inférieure et qui n’est plus une situation d’équilibre et, 3) un équilibre final dans lequel la hauteur d’eau est redevenue nulle du fait de l’égalité de la concentration du soluté de part et d’autre de la membrane.
Remarque 1 Dans l’expérience précédente, une fois l’équilibre atteint (fig. 8), lorsque la hauteur est maximale dans le tube B, on peut avoir l’impression « qu’il ne se passe plus rien». Toutefois, la pression osmotique est toujours présente. Le flux d’eau s’annule du fait d’un équilibre entre la pression osmotique qui a tendance à faire rentrer l’eau dans B et la pression de la colonne liquide qui au contraire à tendance à chasser l’eau de B.
Remarque 2. On peut toujours calculer la pression osmotique d’une solution quelconque à l’aide d’une des formules ci-dessus. Mais, aussi longtemps qu’il n’y a pas de membrane, il ne s’agit alors que d’une pression virtuelle. La pression osmotique « effective », qui se manifeste entre deux compartiments séparés par une membrane, dépend non seulement de la concentration des solutés, mais aussi des propriétés de la membrane. Cette dernière agit donc comme un filtre modifiant la composition de la solution. Cette influence de la membrane se traduit par un paramètre, caractéristique de celle-ci, qu’on appelle son coefficient de réflexion.
Remarque 3. Pression osmotique et pression gazeuse. Historiquement la première loi empirique donnant la valeur de la pression osmotique d’une solution (équation dite de van ‘t Hoff) a été établie, on l’a vu, par référence à la loi des gaz parfaits. Van ‘t Hoff a en effet supposé que les molécules de soluté dans une solution étaient analogues aux molécules de gaz dans un volume limité. En fait l’analogie formelle sur ce point précis n’autorise en aucune façon à pousser plus loin cette similitude entre pression osmotique et pression gazeuse. Comme l’a fait remarquer Duclaux (1938) il y a entre ces deux types de pression, la différence essentielle que la pression gazeuse est toujours une pression réelle, tandis que la pression osmotique est, dans certaines conditions, une pression « potentielle, virtuelle ou latente ». La figure 14 illustre cette différence.

Figure 14. Limites de l’analogie entre la pression osmotique et la pression gazeuse. a) Un ballon d’un litre est supposé contenir 0,1 mole de gaz (ex : 4,4 g de gaz carbonique) à la température de 20°C. La loi de van t’Hoff montre que pour obtenir ce résultat il faut comprimer le gaz à environ 2,4 bars (0,24 MPa). b). Un ballon identique fermé par une membrane hémiperméable M contient une solution déci-normale de saccharose par exemple. Aucune pression hydrostatique n’apparait. c). Si le même ballon est retourné sur un cristallisoir rempli d’eau, il se développera dans le ballon une pression d’environ 2,4 bars comme dans le cas du gaz, ce qui risque de faire éclater au moins la membrane !
La notion de potentiel hydrique que nous abordons maintenant permet de lever cette ambiguïté. Il n’est alors plus question de pression mais d’état énergétique de l’eau. De ce point de vue, le phénomène d’osmose résulte de l’abaissement de potentiel hydrique dû à la présence d’un soluté et le passage spontané de l’eau de A vers B dans l’expérience de l’osmomètre traduit la tendance universelle à l’équilibre des potentiels. Le potentiel hydrique dont la définition découle de la thermodynamique a une signification beaucoup plus générale et un domaine d’application beaucoup plus ample que la pression osmotique ; cette notion peut dès lors apparaître obsolète voire inutile.
Retour aux contenus
Sommaire :
- I. OUTILS ET CONCEPTS DE BASE
- II. ETATS ET TRANSFERTS HYDRIQUES DANS ET À TRAVERS LA PLANTE
- II.1. La cellule en tant que compartiment hydrique
- Introduction : la cellule végétale vivante
- Le potentiel hydrique de la cellule et ses composantes.
- Relation potentiel hydrique – volume cellulaire : le diagramme de Höfler
- L’osmorégulation
- Les transferts d’eau transmembranaires
- Importance des relations hydriques pour l’expansion cellulaire
- Mesure des composantes du potentiel hydrique cellulaire
- Références bibliographiques
- II.2. Anatomie des voies de transfert de l’eau dans la plante
- II.3. L'eau dans les tissus et les organes de la plante et ses méthodes de caractérisation
- II.4. L’absorption de l'eau du sol par les racines
- II.5. La transpiration foliaire
- II.6. Transferts et états hydriques dans le continuum Sol-Plante-Atmosphère
- II.7. L’architecture hydraulique, la cavitation et l’embolie des plantes
- II.8. Un modèle simple de fonctionnement hydrique à l'échelle de la plante entière. Application pour un arbre
- II.9. Les flux de sève dans la plante : couplage entre xylème et phloème, modélisation
- II.10. L’eau et le métabolisme carboné : C3/C4, CAM ; efficience de l’eau
- II.1. La cellule en tant que compartiment hydrique
- III. FONCTIONNEMENT DES VEGETAUX EN SITUATION DE STRESS LIE A L’EAU
- III.1. Les végétaux face à la sécheresse
- III.2. Efficience agronomique de l’eau
- Les composantes de l’efficience d’utilisation de l’eau par les cultures.
- Nécessité de quantifier séparément Evaporation du sol et Transpiration des plantes
- Les interactions entre nutrition azotée et alimentation hydrique, conséquence sur l’efficience d’utilisation de l’eau par les cultures.
- Références bibliographiques
- IV. AGRONOMIE DE L’EAU